7  Appointment scheduling heuristics

7.1 Objective

In this experiment, we will test the validity of existing appointment scheduling heuristics by evaluating several instances of scheduling systems and analyzing the results. We will examine the performance of different scheduling strategies and compare them to the heuristics proposed in the literature. The goal is to find quasi optimal schedules that form a good starting point for further optimization using for instance local search algorithms.

7.2 Background

The extensive body of research on appointment scheduling offers valuable heuristics for designing schedules that are likely close to optimal. In their seminal work, Welch et al. (1952)1 established the following rule: schedule two patients at the beginning of the day to minimize the risk of idle time if one patient does not show up. The remaining patients should then be scheduled at intervals equal to the mean consultation time.

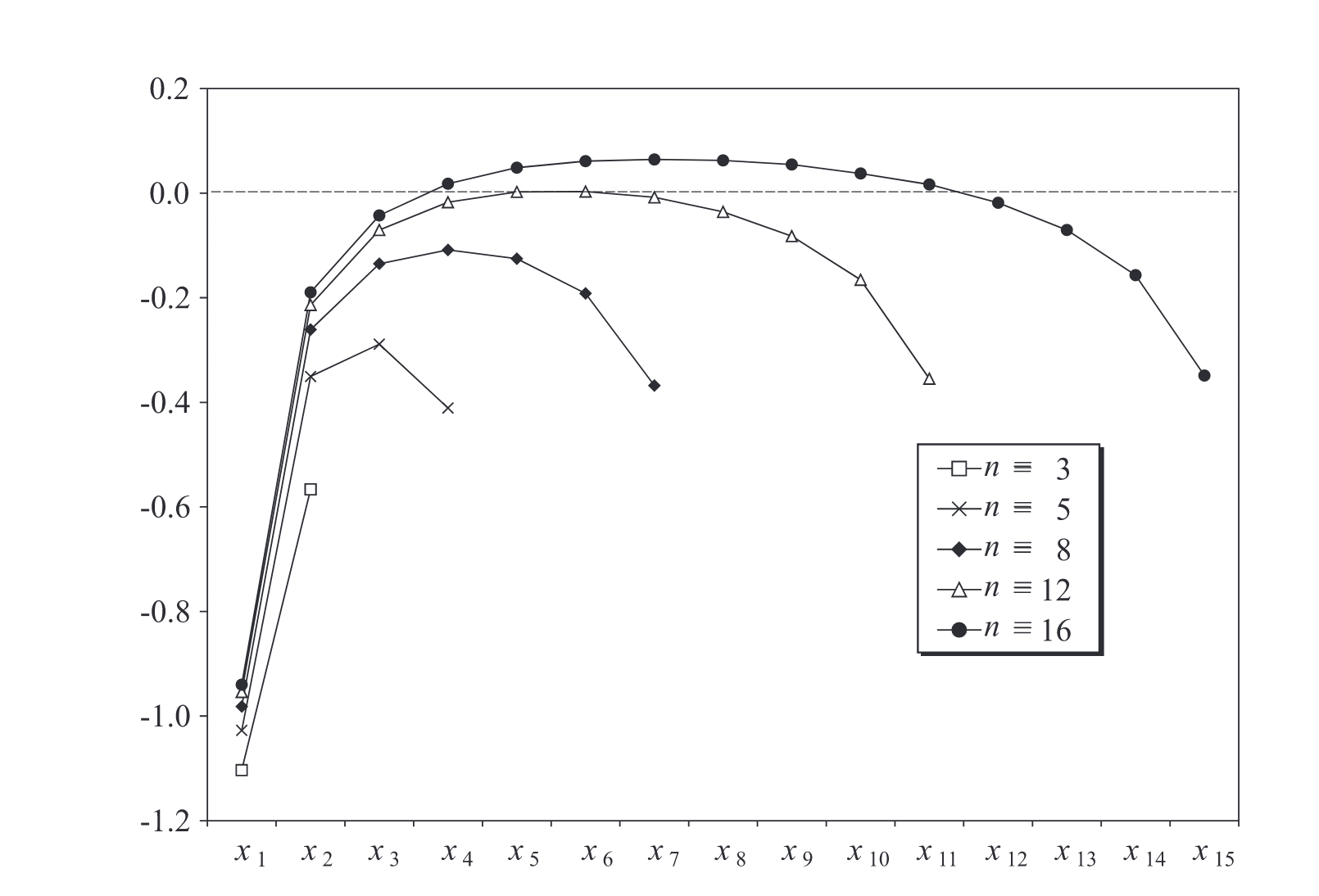
‘Dome’ shapes of appointment schedules. From Robinson and Chen (2003)2

Robinson and Chen (2003)3 explored the structure of optimal schedules. In their model, the length of intervals could be adjusted to accommodate different job allowances. Their findings include the following general observations:

  • Job allowances follow a ‘dome’ pattern, with more time allotted to patients in the middle of the day.
  • The first job allowance is consistently much lower than the subsequent ones, while the final job allowance is also somewhat lower than the others.
  • Intermediate job allowances are generally uniform.

Klassen and Yoogalingam (2009)4 observed a plateau form when appointment intervals are restricted to integers.

In our model, all interval times are fixed integers, but job allowances can be adjusted by overbooking or underbooking selected service intervals. We examined the extent to which the above rules apply to our model definition.

7.3 Methodology

7.3.1 Tools and Materials

import itertools
from joblib import Parallel, delayed
import networkx as nx
import plotly.graph_objects as go
import numpy as np
from typing import List, Tuple
import plotly.subplots as sp
from plotly.subplots import make_subplots
from concurrent.futures import ThreadPoolExecutor
import time
import math
from functions import create_random_schedules, calculate_objective, compute_convolutions, local_search, get_v_star, powerset, get_neighborhood, build_welch_bailey_schedule, service_time_with_no_shows, create_schedule_network, create_schedule_network_var_edges, create_schedule_network_from_lists, local_search_w_intermediates, build_quasi_optimal_schedule

7.3.2 Experimental Design

We have developed a function that uses the Bailey-Welch rule to create a initial schedule.

def build_welch_bailey_schedule(N, T):
    """
    Build a schedule based on the Welch and Bailey (1952) heuristic.

    Parameters:
    N (int): Number of patients to be scheduled.
    T (int): Number of time intervals in the schedule.

    Returns:
    list: A schedule of length T where each item represents the number of patients scheduled
          at the corresponding time interval.
    """
    # Initialize the schedule with zeros
    schedule = [0] * T

    # Schedule the first two patients at the beginning
    schedule[0] = 2
    remaining_patients = N - 2

    # Distribute patients in the middle time slots with gaps
    for t in range(1, T - 1):
        if remaining_patients <= 0:
            break
        if t % 2 == 1:  # Create gaps (only schedule patients at odd time slots)
            schedule[t] = 1
            remaining_patients -= 1

    # Push any remaining patients to the last time slot
    schedule[-1] += remaining_patients

    return schedule

We will compare the performance of the Bailey-Welch heuristic with the performance of a schedule generated by a local search algorithm. The local search algorithm will start from the Bailey-Welch schedule and iteratively improve it by swapping patients between time slots to reduce the patients’ waiting time and physician’s overtime.

7.3.3 Variables

  • Independent Variables:
    • Different schedule designs with increasingly large instances (lengths and number of patients).
  • Dependent Variables:
    • Objective function value (weighted sum of average waiting time and physician’s overtime) for each schedule.
    • Computation times

7.3.4 Samples

We will generate several schedules with different lengths (\(T\)), numbers of patients (\(N\)) and weights for patients’ waiting time (\(w\)) relatively to overtime.

\[ N \in \{16, \dots , 22\} \] \[ T \in \{15, \dots , 20\} \] \[ w \in \{0.1, 0,9\} \] This means that the total solution space varies between 13 mln and 244 bln schedules. The challenge is to find the optimal schedules within these vast solution spaces.

# Graph representation of an appointment schedule

# Define parameters
N = 4  # Number of patients
T = 3  # Number of time intervals
s = [0.3, 0.2, 0.1, 0.05, 0.15, 0.2]  # Example service time probability distribution
d = 2  # Duration threshold
q = 0.1  # No-show probability
w = 0.5  # Weight for waiting time in the objective

# Create and visualize the network
fig = create_schedule_network(N=N, T=T, s=s, d=d, q=q, w=w, echo=True)
fig.show()
Schedule: (0, 0, 4), Objective: 4.36, Expected mean waiting time: 11.61, Expected spillover time: 5.81
Schedule: (0, 1, 3), Objective: 3.43, Expected mean waiting time: 8.37, Expected spillover time: 4.77
Schedule: (0, 2, 2), Objective: 3.21, Expected mean waiting time: 8.42, Expected spillover time: 4.31
Schedule: (0, 3, 1), Objective: 3.28, Expected mean waiting time: 9.79, Expected spillover time: 4.12
Schedule: (0, 4, 0), Objective: 3.48, Expected mean waiting time: 11.61, Expected spillover time: 4.06
Schedule: (1, 0, 3), Objective: 2.86, Expected mean waiting time: 6.35, Expected spillover time: 4.14
Schedule: (1, 1, 2), Objective: 2.44, Expected mean waiting time: 5.58, Expected spillover time: 3.48
Schedule: (1, 2, 1), Objective: 2.43, Expected mean waiting time: 6.64, Expected spillover time: 3.21
Schedule: (1, 3, 0), Objective: 2.60, Expected mean waiting time: 8.37, Expected spillover time: 3.11
Schedule: (2, 0, 2), Objective: 2.36, Expected mean waiting time: 6.03, Expected spillover time: 3.20
Schedule: (2, 1, 1), Objective: 2.27, Expected mean waiting time: 6.79, Expected spillover time: 2.85
Schedule: (2, 2, 0), Objective: 2.41, Expected mean waiting time: 8.42, Expected spillover time: 2.72
Schedule: (3, 0, 1), Objective: 2.40, Expected mean waiting time: 8.24, Expected spillover time: 2.75
Schedule: (3, 1, 0), Objective: 2.52, Expected mean waiting time: 9.79, Expected spillover time: 2.59
Schedule: (4, 0, 0), Objective: 2.74, Expected mean waiting time: 11.61, Expected spillover time: 2.57

7.3.5 Experimental Procedure

We will evaluate multiple schedules using the Bailey-Welch heuristic and a local search algorithm, complemented by visualizations to compare their structures. Additionally, we will analyze computation times to assess the practical feasibility of the local search algorithm for large-scale instances.

7.4 Results

We began with a set of relatively small instances, keeping the number of intervals fixed while varying the number of patients. For each instance, we applied the local search algorithm and compared the resulting optimized schedules to the initial ones. The initial schedules, generated using the Bailey-Welch heuristic, are depicted as blue dotted lines, while the optimized schedules obtained through local search are shown as red solid lines.

from functions import create_random_schedules, calculate_objective, compute_convolutions, local_search, get_v_star, powerset, get_neighborhood, build_welch_bailey_schedule

# Assuming the necessary functions are defined elsewhere:
# get_v_star, build_welch_bailey_schedule, compute_convolutions, local_search

# Parameters
N = range(16, 20)
T = 15
s = [0.3, 0.2, 0.1, 0.05, 0.15, 0.2]  # Example service time probability distribution
d = 2  # Duration threshold
q = 0.1  # No-show probability
w = 0.1  # Weight for waiting time in the objective
v_star = get_v_star(T)

# Lists to store results
x_stars = []
x_initials = []  # To store initial schedules
obj_vals = []
schedules_list, objectives_list = [], []

# Iterate over each n in N
start = time.time()
for n in N:
    print(f'Running local search for schedule with N={n}')
    x = build_welch_bailey_schedule(n, T)
    x_initials.append(x)  # Store the initial schedule
    convolutions = compute_convolutions(s, n, q)
    schedules, objectives = local_search_w_intermediates(x, d, convolutions, w, v_star, T)
    #x_star, obj = local_search(x, d, q, convolutions, w, v_star, T)
    obj_vals.append(objectives[-1])
    x_stars.append(schedules[-1])
    schedules_list.append(schedules)
    objectives_list.append(objectives)
end = time.time()
print("Optimized schedules:", x_stars)
print("Objective values:", obj_vals)
print(f"Search time: {end - start:.2f} seconds")
Running local search for schedule with N=16
Total evaluations: 36913
Running local search for schedule with N=17
Total evaluations: 33123
Running local search for schedule with N=18
Total evaluations: 33123
Running local search for schedule with N=19
Total evaluations: 33123
Optimized schedules: [[2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2], [2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 3], [2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 4]]
Objective values: [10.209161916511897, 12.537501602843756, 15.121828179211807, 17.927771231270906]
Search time: 57.26 seconds
# Number of subplots needed
num_subplots = len(x_stars)

# Create a subplot figure with one chart per subplot
fig = sp.make_subplots(
    rows=num_subplots, 
    cols=1, 
    shared_xaxes=True, 
    subplot_titles=[f'n = {n}' for n in N]
)

# Add each initial and optimized schedule to its respective subplot
for idx, (x_initial, x_star) in enumerate(zip(x_initials, x_stars)):
    # Add initial schedule as a dotted line
    fig.add_trace(
        go.Scatter(
            x=list(range(T)), 
            y=x_initial, 
            mode='lines', 
            name='Initial schedule' if idx == 0 else None,  # Show legend only once
            line=dict(dash='dot', color='blue')
        ), 
        row=idx + 1, 
        col=1
    )
    
    # Add optimized schedule as a solid line with markers
    fig.add_trace(
        go.Scatter(
            x=list(range(T)), 
            y=x_star, 
            mode='lines+markers', 
            name='Optimized schedule' if idx == 0 else None,  # Show legend only once
            line=dict(color='red')
        ), 
        row=idx + 1, 
        col=1
    )

# Update layout properties
fig.update_layout(
    height=600 * num_subplots,  # Adjust height based on the number of subplots
    title=dict(
        text=f"Optimal schedules across different values of N\n(T={T}, w={w})",
        x=0.5,  # Center the title horizontally
        # y=0.95,  # Adjust the vertical position (closer to the top)
        font=dict(size=20),  # Optional: Adjust title font size
        pad=dict(b=50)  # Add padding at the top of the title
    ),
    xaxis_title="Time slot (x)",
    yaxis_title="# of patients (y)",
    template="plotly_white",
    showlegend=False  # Enable legend to distinguish between initial and optimized schedules
)

# Set consistent y-axis ticks for each subplot
for i in range(1, num_subplots + 1):
    fig.update_yaxes(tickmode='linear', tick0=0, dtick=1, row=i, col=1)

# Optionally, adjust the legend position
fig.update_layout(legend=dict(
    orientation="h",
    yanchor="bottom",
    y=1.02,
    xanchor="right",
    x=1
))

# Show the Plotly figure
fig.show()

Subsequently we’ve analyzed the number of steps required for the local search algorithm to transition from the initial schedule to the optimal schedule, as well as the characteristics of the search paths. To accomplish this, we’ve recorded and visualized the search paths using graph representations for multiple instances starting at the initial schedule and ending at the optimized schedule. Each node in the graph represents an improved schedule. The length of the edges corresponds to the improvement in the objective function value.

for idx, (n, schedules, objectives) in enumerate(zip(N, schedules_list, objectives_list), start=1):
    print(f'Processing N={n}, number of schedules: {len(schedules)}')
    
    # Create individual network graph
    individual_fig = create_schedule_network_from_lists(
        schedules=schedules,
        objective_values=objectives,
        echo=False
    )
    
    individual_fig.update_layout(
        autosize=False,
        width=1500,
        height=1800,
        margin=dict(
            l=50,
            r=50,
            b=100,
            t=100,
            pad=4
        )
    )
    
    # Show the individual network graph
    individual_fig.show()
Processing N=16, number of schedules: 39
Processing N=17, number of schedules: 43
Processing N=18, number of schedules: 43
Processing N=19, number of schedules: 43

Next we’ve repeated the experiment for similar instances but with a higher weight for the waiting time in the objective function. In this case we also implemented parallel processing to speed up the computation.

# Function to process a single N
def process_schedule(n, T, s, d, q, w, v_star):
    print(f'Running local search for schedule with N={n}')
    x = build_welch_bailey_schedule(n, T)
    convolutions = compute_convolutions(s, n, q)
    schedules, objectives = local_search_w_intermediates(x, d, convolutions, w, v_star, T)
    return {
        'n': n,
        'x_initial': x,
        'schedules': schedules,
        'objectives': objectives,
        'x_star': schedules[-1],
        'obj_val': objectives[-1],
    }

# Parameters
N = range(16, 20)
T = 15
s = [0.3, 0.2, 0.1, 0.05, 0.15, 0.2]  # Example service time probability distribution
d = 2  # Duration threshold
q = 0.1  # No-show probability
w = 0.9  # Weight for waiting time in the objective
v_star = get_v_star(T)

# Lists to store results
results = []

start = time.time()

# Parallelize the process_schedule function using Joblib
results = Parallel(n_jobs=-1)(delayed(process_schedule)(n, T, s, d, q, w, v_star) for n in N)

end = time.time()

# Extract results
x_initials = [result['x_initial'] for result in results]
schedules_list = [result['schedules'] for result in results]
objectives_list = [result['objectives'] for result in results]
x_stars = [result['x_star'] for result in results]
obj_vals = [result['obj_val'] for result in results]

print("Optimized schedules:", x_stars)
print("Objective values:", obj_vals)
print(f"Search time: {end - start:.2f} seconds")
Optimized schedules: [[2, 0, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 4], [2, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 4], [2, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 5], [2, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 6]]
Objective values: [39.1854102224129, 48.66396904640554, 58.95723399701313, 70.90032316773812]
Search time: 16.10 seconds
# Number of subplots needed
num_subplots = len(x_stars)

# Create a subplot figure with one chart per subplot
fig = sp.make_subplots(
    rows=num_subplots, 
    cols=1, 
    shared_xaxes=True, 
    subplot_titles=[f'n = {n}' for n in N]
)

# Add each initial and optimized schedule to its respective subplot
for idx, (x_initial, x_star) in enumerate(zip(x_initials, x_stars)):
    # Add initial schedule as a dotted line
    fig.add_trace(
        go.Scatter(
            x=list(range(T)), 
            y=x_initial, 
            mode='lines', 
            name='Initial schedule' if idx == 0 else None,  # Show legend only once
            line=dict(dash='dot', color='blue')
        ), 
        row=idx + 1, 
        col=1
    )
    
    # Add optimized schedule as a solid line with markers
    fig.add_trace(
        go.Scatter(
            x=list(range(T)), 
            y=x_star, 
            mode='lines+markers', 
            name='Optimized schedule' if idx == 0 else None,  # Show legend only once
            line=dict(color='red')
        ), 
        row=idx + 1, 
        col=1
    )

# Update layout properties
fig.update_layout(
    height=600 * num_subplots,  # Adjust height based on the number of subplots
    title=dict(
        text=f"Optimal schedules across different values of N\n(T={T}, w={w})",
        x=0.5,  # Center the title horizontally
        # y=0.95,  # Adjust the vertical position (closer to the top)
        font=dict(size=20),  # Optional: Adjust title font size
        pad=dict(b=50)  # Add padding at the top of the title
    ),
    xaxis_title="Time slot (x)",
    yaxis_title="# of patients (y)",
    template="plotly_white",
    showlegend=False  # Enable legend to distinguish between initial and optimized schedules
)

# Set consistent y-axis ticks for each subplot
for i in range(1, num_subplots + 1):
    fig.update_yaxes(tickmode='linear', tick0=0, dtick=1, row=i, col=1)

# Optionally, adjust the legend position
fig.update_layout(legend=dict(
    orientation="h",
    yanchor="bottom",
    y=1.02,
    xanchor="right",
    x=1
))

# Show the Plotly figure
fig.show()
for idx, (n, schedules, objectives) in enumerate(zip(N, schedules_list, objectives_list), start=1):
    print(f'Processing N={n}, number of schedules: {len(schedules)}')
    
    # Create individual network graph
    individual_fig = create_schedule_network_from_lists(
        schedules=schedules,
        objective_values=objectives,
        echo=False
    )
    
    individual_fig.update_layout(
        autosize=False,
        width=1500,
        height=1800,
        margin=dict(
            l=50,
            r=50,
            b=100,
            t=100,
            pad=4
        )
    )
    
    # Show the individual network graph
    individual_fig.show()
Processing N=16, number of schedules: 20
Processing N=17, number of schedules: 21
Processing N=18, number of schedules: 26
Processing N=19, number of schedules: 27

Finally we’ve expanded the experiment to include larger instances. We’ve increased the number of intervals and patients, while keeping the weight for the waiting time in the objective function at 0.9.

# Function to process a single N
def process_schedule(n, T, s, d, w, v_star):
    print(f'Running local search for schedule with N={n}')
    x = build_quasi_optimal_schedule(n, T)
    convolutions = compute_convolutions(s, n, q)
    schedules, objectives = local_search_w_intermediates(x, d, convolutions, w, v_star, T)
    return {
        'n': n,
        'x_initial': x,
        'schedules': schedules,
        'objectives': objectives,
        'x_star': schedules[-1],
        'obj_val': objectives[-1],
    }

# Parameters
N = range(21, 24)
T = 20
s = [0.3, 0.2, 0.1, 0.05, 0.15, 0.2]  # Example service time probability distribution
d = 2  # Duration threshold
q = 0.1  # No-show probability
w = 0.5  # Weight for waiting time in the objective
v_star = get_v_star(T)

# Lists to store results
results = []

start = time.time()

# Parallelize the process_schedule function using Joblib
results = Parallel(n_jobs=-1)(delayed(process_schedule)(n, T, s, d, w, v_star) for n in N)

end = time.time()

# Extract results
x_initials = [result['x_initial'] for result in results]
schedules_list = [result['schedules'] for result in results]
objectives_list = [result['objectives'] for result in results]
x_stars = [result['x_star'] for result in results]
obj_vals = [result['obj_val'] for result in results]

print("Optimized schedules:", x_stars)
print("Objective values:", obj_vals)
print(f"Search time: {end - start:.2f} seconds")
Running local search for schedule with N=18
Total evaluations: 18625
Running local search for schedule with N=17
Total evaluations: 19548
Running local search for schedule with N=19
Total evaluations: 18633
Optimized schedules: [[2, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 4], [2, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 5], [2, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 5]]
Objective values: [36.303606121519586, 42.87410729585329, 50.14956668757205]
Search time: 338.51 seconds
# Number of subplots needed
num_subplots = len(x_stars)

# Create a subplot figure with one chart per subplot
fig = sp.make_subplots(
    rows=num_subplots, 
    cols=1, 
    shared_xaxes=True, 
    subplot_titles=[f'n = {n}' for n in N]
)

# Add each initial and optimized schedule to its respective subplot
for idx, (x_initial, x_star) in enumerate(zip(x_initials, x_stars)):
    # Add initial schedule as a dotted line
    fig.add_trace(
        go.Scatter(
            x=list(range(T)), 
            y=x_initial, 
            mode='lines', 
            name='Initial schedule' if idx == 0 else None,  # Show legend only once
            line=dict(dash='dot', color='blue')
        ), 
        row=idx + 1, 
        col=1
    )
    
    # Add optimized schedule as a solid line with markers
    fig.add_trace(
        go.Scatter(
            x=list(range(T)), 
            y=x_star, 
            mode='lines+markers', 
            name='Optimized schedule' if idx == 0 else None,  # Show legend only once
            line=dict(color='red')
        ), 
        row=idx + 1, 
        col=1
    )

# Update layout properties
fig.update_layout(
    height=600 * num_subplots,  # Adjust height based on the number of subplots
    title=dict(
        text=f"Optimal schedules across different values of N\n(T={T}, w={w})",
        x=0.5,  # Center the title horizontally
        y=0.95,  # Adjust the vertical position (closer to the top)
        font=dict(size=20),  # Optional: Adjust title font size
        pad=dict(t=50)  # Add padding at the top of the title
    ),
    xaxis_title="Time slot (x)",
    yaxis_title="# of patients (y)",
    template="plotly_white",
    showlegend=False  # Enable legend to distinguish between initial and optimized schedules
)

# Set consistent y-axis ticks for each subplot
for i in range(1, num_subplots + 1):
    fig.update_yaxes(tickmode='linear', tick0=0, dtick=1, row=i, col=1)

# Optionally, adjust the legend position
fig.update_layout(legend=dict(
    orientation="h",
    yanchor="bottom",
    y=1.02,
    xanchor="right",
    x=1
))

# Show the Plotly figure
fig.show()
for idx, (n, schedules, objectives) in enumerate(zip(N, schedules_list, objectives_list), start=1):
    print(f'Processing N={n}, number of schedules: {len(schedules)}')
    
    # Create individual network graph
    individual_fig = create_schedule_network_from_lists(
        schedules=schedules,
        objective_values=objectives,
        echo=False
    )
    
    individual_fig.update_layout(
        autosize=False,
        width=1500,
        height=1800,
        margin=dict(
            l=50,
            r=50,
            b=100,
            t=100,
            pad=4
        )
    )
    
    # Show the individual network graph
    individual_fig.show()
Processing N=21, number of schedules: 2
Processing N=22, number of schedules: 2
Processing N=23, number of schedules: 8

7.5 Discussion

The results of the experiments appear to confirm that optimal schedules adhere to the Bailey-Welch rule of scheduling two patients at the start of the day. The remaining patients are then allocated as evenly as possible across the remaining time intervals. When patients’ time is valued higher than the physician’s, empty intervals are inserted into the schedule to absorb potential spillover times. This adjustment, however, pushes some patients out of the schedule, thereby increasing the total overtime.

The local search algorithm required on average 22 and 42 steps for both types of small instances (\(w = 0.1\) and \(w = 0.9\), respectively) to compute the global optimum. Interestingly the number of steps required to reach the optimal schedule did not increase significantly for the larger instance (\(T=20\), \(N=\{21, 22\}\), \(w = 0.9\)), despite the larger solution space. This suggests that the local search algorithm is effective in finding the optimal schedule within a reasonable number of steps.

In each instance, the most significant reductions in the objective value occurred each time a patient was moved from the last time interval to an earlier one. This adjustment minimized overtime, which apparently has a substantial impact on the objective value.

7.6 Timeline

This experiment was started at 18-11-2024 and is expected to be completed by 31-12-2024.

7.7 References

  1. Welch, J. D., & Bailey, N. T. J. (1952). Appointment systems in hospital outpatient departments. The Lancet, 259(6718), 1105-1108.↩︎

  2. Robinson, L. W., & Chen, R. R. (2003). Scheduling doctors’ appointments: optimal and empirically-based heuristic policies. IIE Transactions, 35(3), 295-307.↩︎

  3. Robinson, L. W., & Chen, R. R. (2003). Scheduling doctors’ appointments: optimal and empirically-based heuristic policies. IIE Transactions, 35(3), 295-307.↩︎

  4. Klassen, K. J., & Yoogalingam, R. (2009). Improving performance in outpatient appointment services with a simulation optimization approach. Production and Operations Management, 18(4), 447-458.↩︎