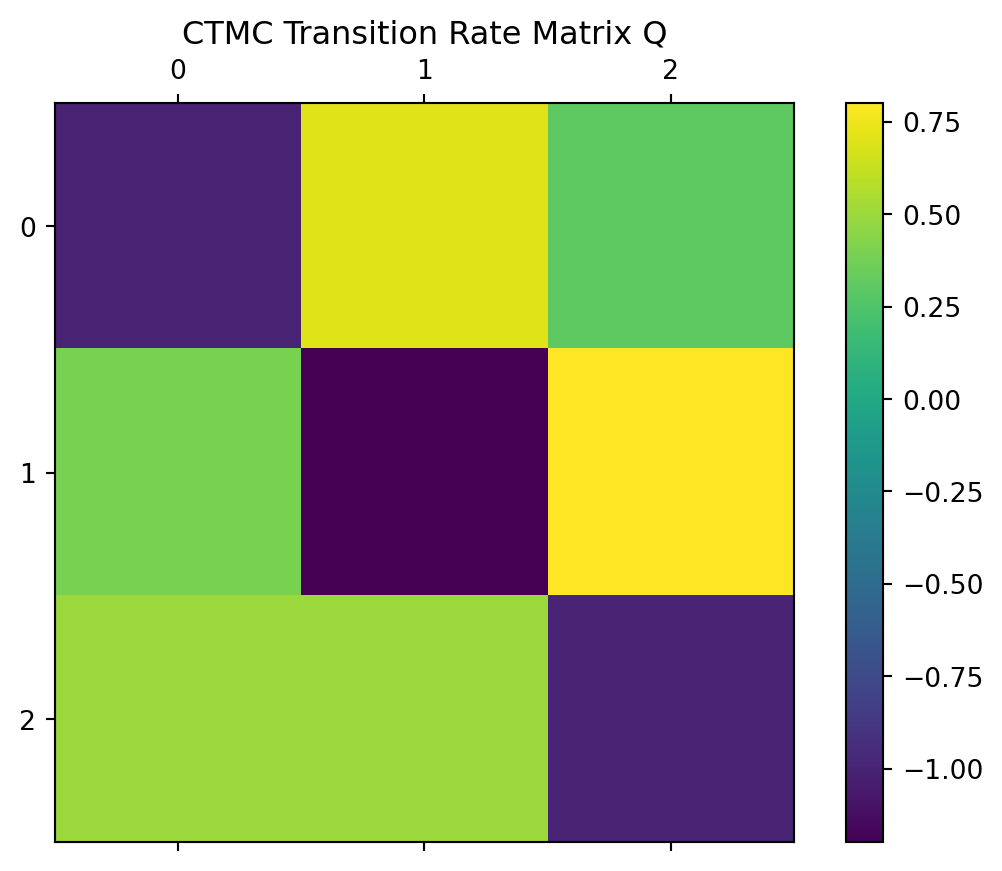
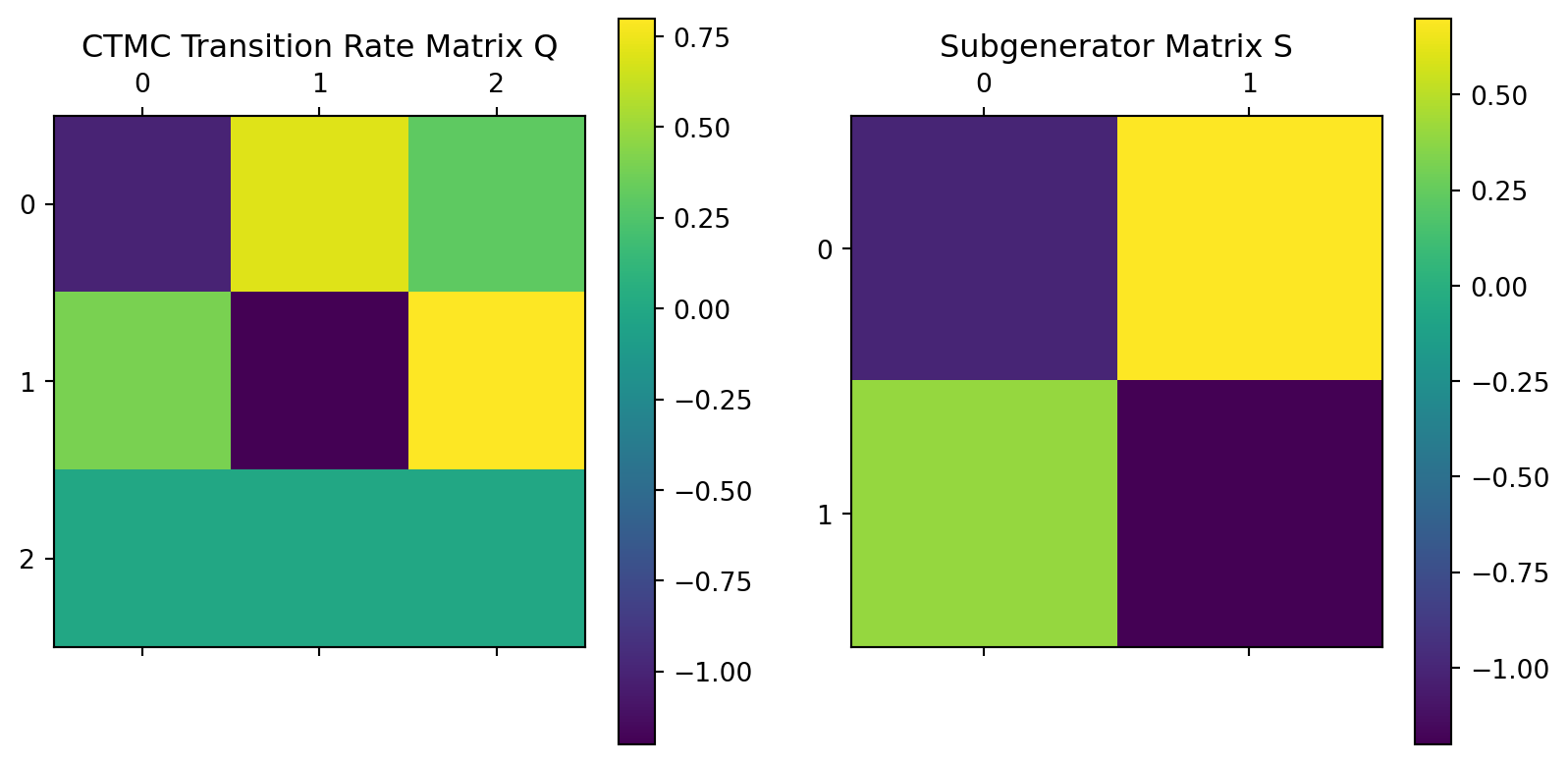
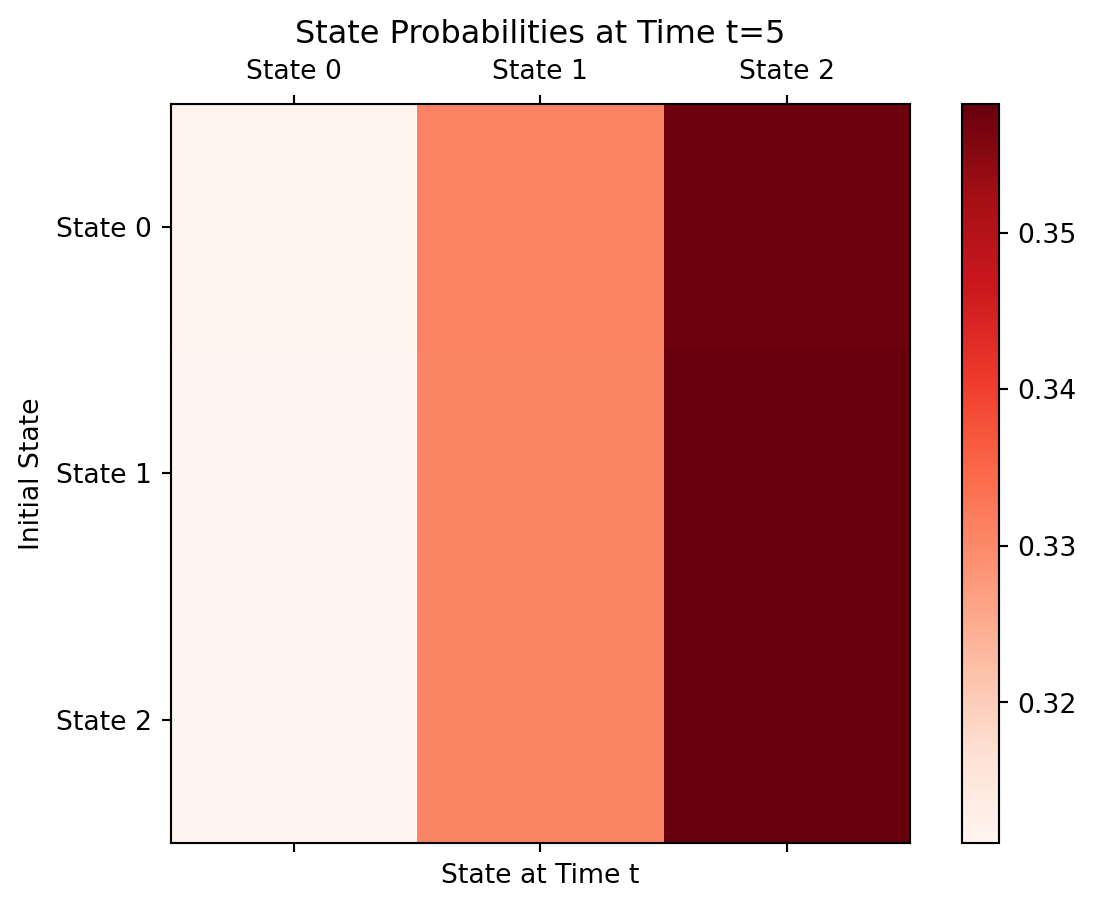
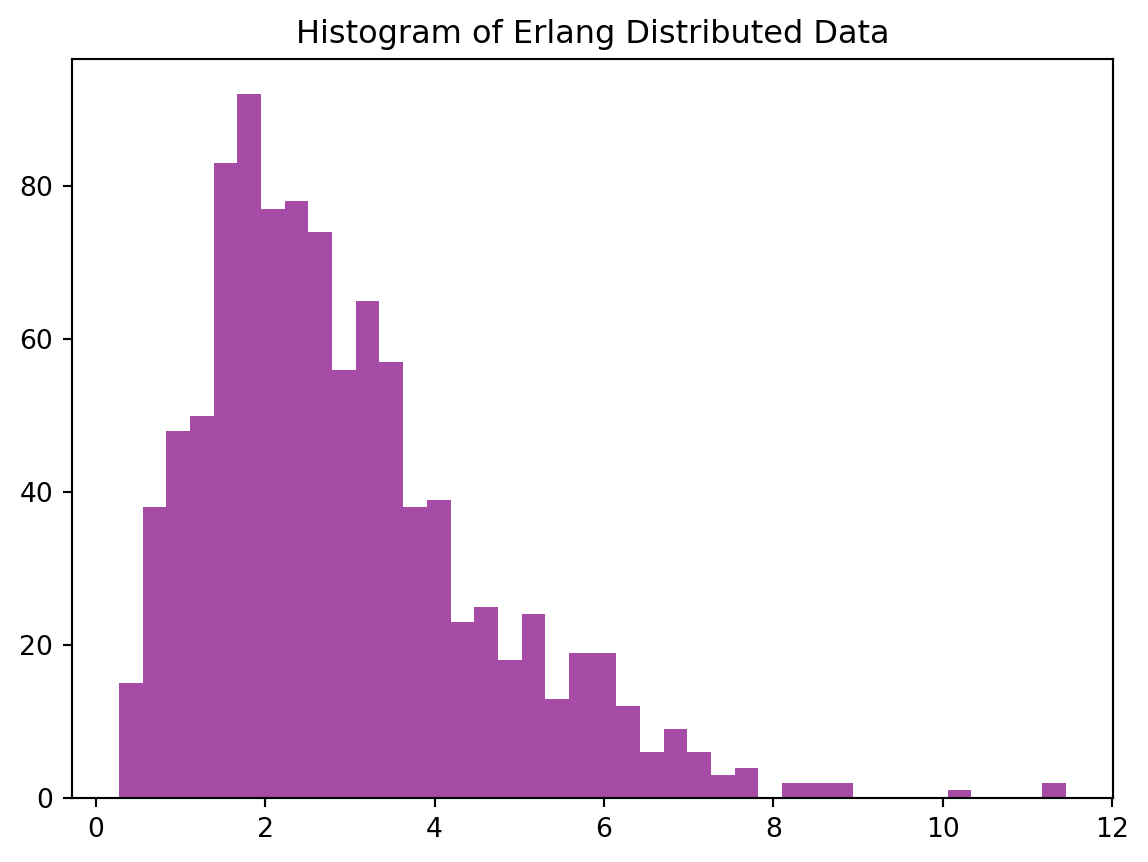
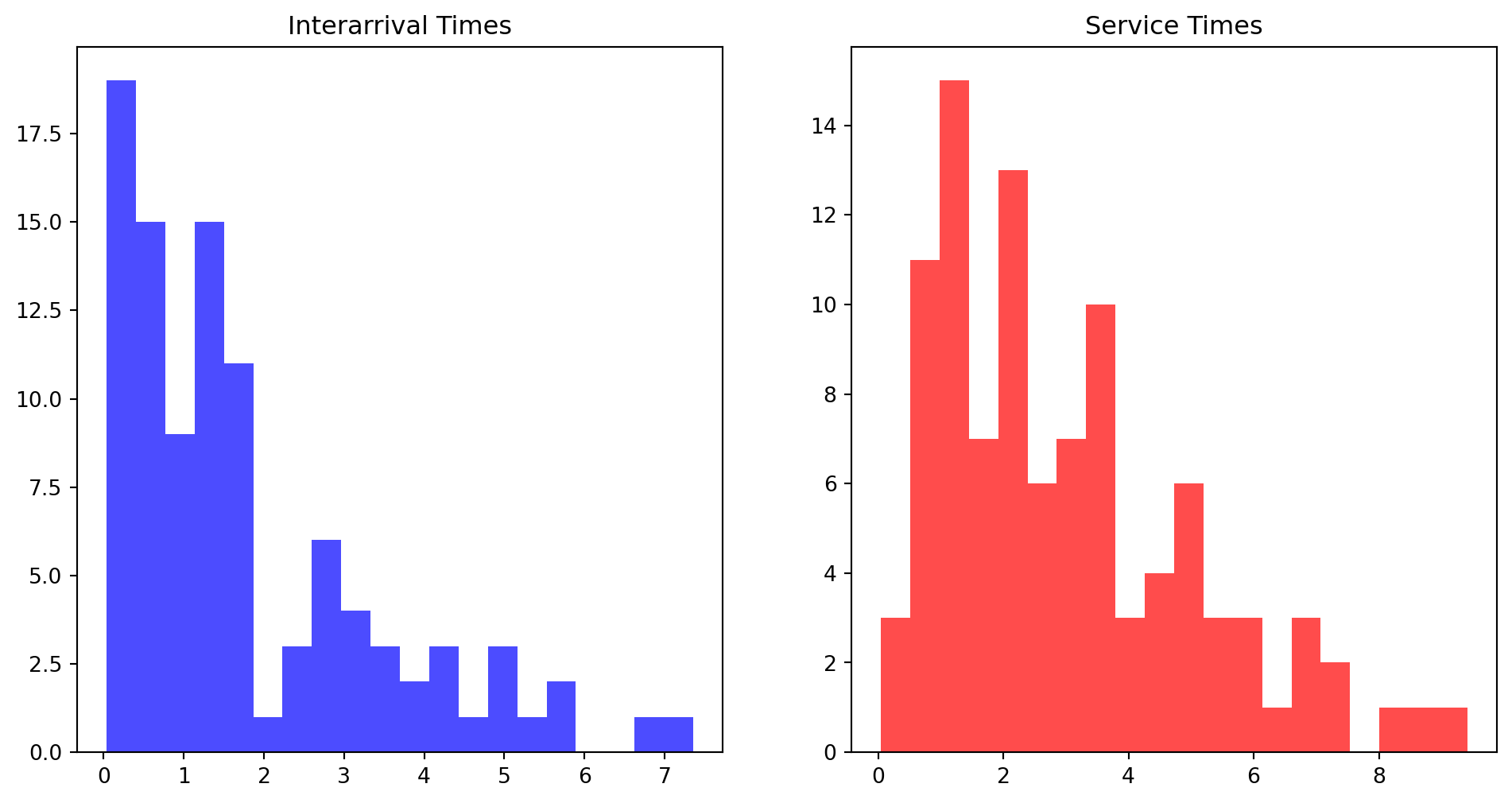
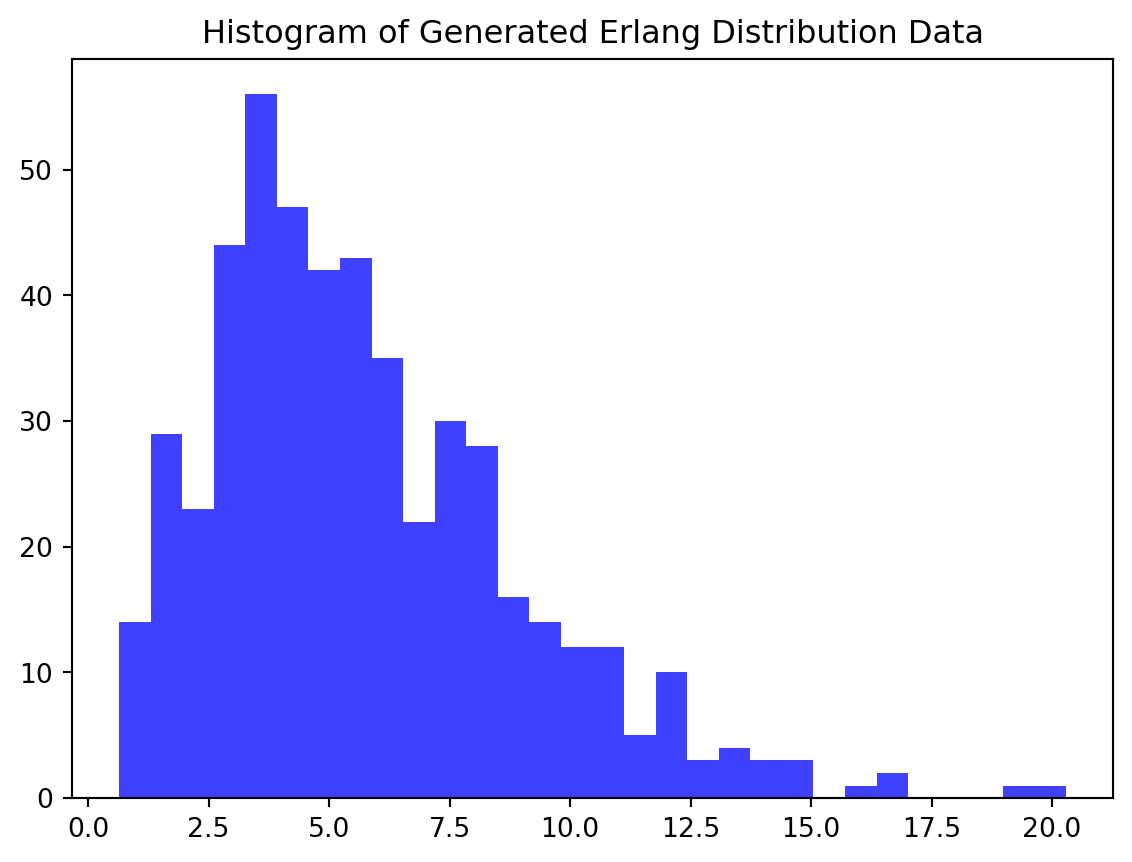
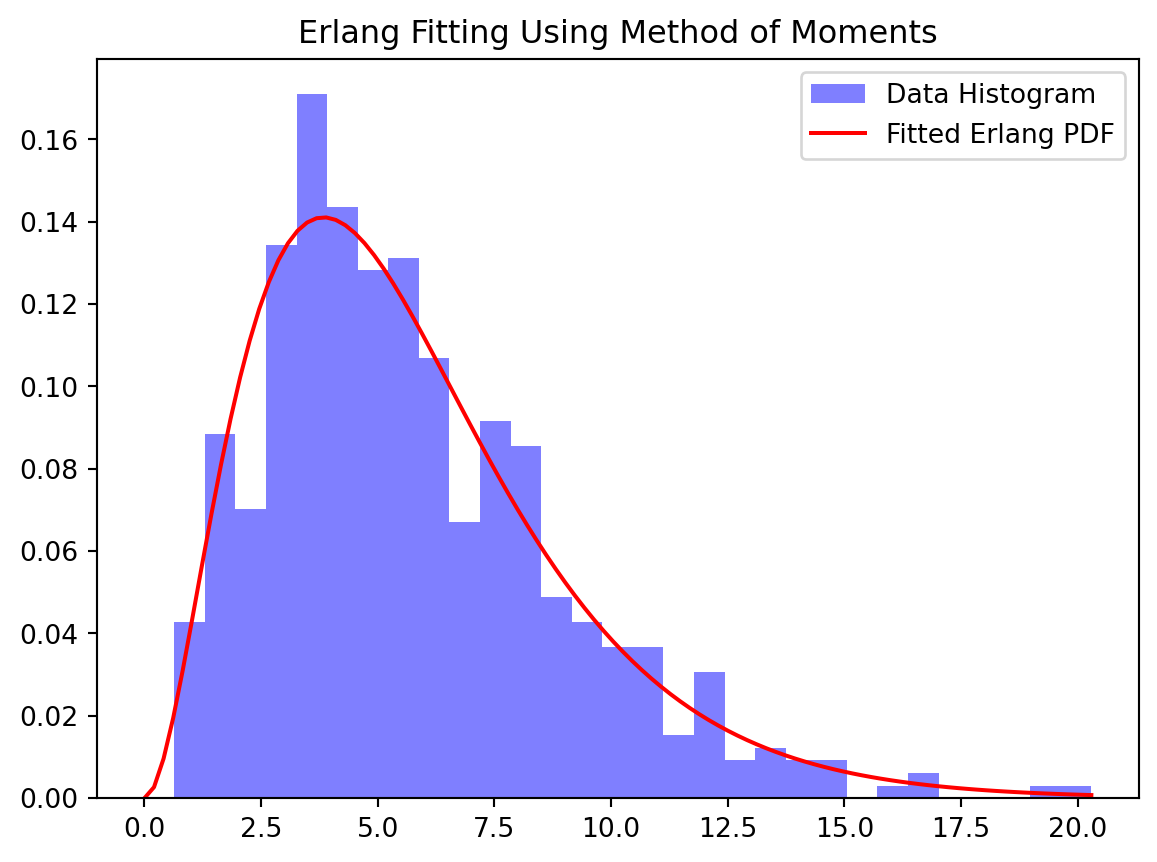
[100, 0, 100, 100, 0, 0, 0, 0, 0, 100, 0, 0, 0, 100, 0, 0, 100, 0, 0, 100, 0, 100, 100, 0, 0, 100, 100, 100, 0, 0, 100, 100, 100, 100, 0, 0, 0, 100, 0, 0, 100, 0, 100, 0, 0, 0, 0, 100, 0, 0, 100, 100, 0, 100, 100, 0, 100, 0, 100, 100, 0, 0, 100, 100, 0, 100, 100, 0, 0, 100, 100, 100, 0, 0, 100, 100, 100, 0, 100, 100, 0, 100, 0, 100, 0, 0, 100, 0, 0, 100, 100, 0, 0, 100, 100, 100, 100, 100, 0, 100, 0, 0, 0, 100, 100, 0, 0, 0, 0, 100, 0, 100, 100, 100, 100, 0, 100, 0, 0, 0, 100, 0, 100, 0, 0, 0, 100, 100, 100, 100, 100, 100, 100, 100, 0, 100, 100, 0, 100, 100, 100, 100, 100, 0, 100, 100, 0, 0, 0, 100, 100, 100, 100, 0, 100, 0, 0, 100, 100, 0, 0, 0, 100, 100, 100, 0, 0, 0, 100, 0, 100, 100, 100, 0, 100, 100, 100, 0, 0, 100, 100, 0, 0, 0, 0, 100, 100, 0, 0, 100, 100, 0, 100, 100, 100, 100, 100, 0, 100, 0, 100, 100, 0, 100, 0, 0, 0, 0, 0, 100, 0, 0, 0, 0, 0, 100, 100, 100, 0, 0, 0, 100, 0, 100, 100, 0, 100, 100, 0, 100, 100, 100, 100, 100, 100, 0, 0, 0, 100, 0, 100, 100, 0, 100, 100, 0, 0, 0, 100, 100, 100, 100, 100, 0, 100, 100, 100, 0, 0, 100, 100, 100, 100, 0, 100, 0, 100, 0, 0, 100, 100, 100, 0, 100, 100, 100, 100, 0, 100, 0, 100, 100, 0, 100, 0, 100, 100, 0, 100, 100, 100, 100, 100, 100, 0, 0, 100, 0, 100, 100, 0, 100, 100, 0, 0, 0, 100, 0, 0, 100, 0, 0, 100, 100, 0, 100, 0, 100, 100, 100, 0, 100, 100, 100, 100, 0, 0, 0, 100, 0, 100, 0, 100, 0, 0, 0, 0, 100, 100, 0, 100, 100, 0, 0, 100, 0, 0, 100, 0, 100, 100, 100, 100, 0, 100, 100, 0, 100, 0, 100, 0, 100, 100, 0, 0, 0, 100, 100, 0, 100, 100, 0, 100, 100, 0, 0, 0, 0, 100, 0, 0, 100, 0, 0, 0, 0, 100, 0, 100, 100, 100, 0, 100, 0, 100, 0, 0, 100, 100, 100, 0, 0, 100, 100, 0, 0, 0, 0, 100, 0, 100, 100, 100, 100, 100, 100, 100, 0, 100, 0, 0, 100, 0, 0, 0, 100, 0, 100, 0, 100, 100, 100, 0, 0, 0, 0, 100, 0, 0, 0, 100, 100, 100, 100, 0, 0, 100, 100, 0, 100, 0, 0, 0, 0, 100, 0, 100, 0, 100, 0, 0, 0, 100, 0, 0, 100, 100, 100, 100, 0, 0, 0, 100, 0, 100, 100, 100, 0, 0, 0, 100, 0, 100, 0, 0, 0, 100, 100, 0, 100, 0, 100, 100, 100, 100, 0, 100, 0, 0, 100, 0, 0, 0, 0, 0, 0, 100, 0, 100, 100, 0, 0, 0, 0, 100, 100, 0, 0, 0, 0, 0, 100, 0, 100, 100, 100, 0, 0, 100, 0, 100, 100, 0, 0, 100, 100, 100, 100, 0, 100, 0, 0, 100, 100, 100, 0, 0, 0, 0, 100, 0, 0, 100, 0, 0, 0, 100, 0, 0, 100, 100, 100, 0, 100, 0, 100, 0, 0, 0, 100, 0, 0, 0, 100, 0, 0, 0, 100, 0, 100, 0, 0, 0, 100, 100, 0, 0, 100, 100, 0, 100, 100, 0, 100, 100, 0, 100, 100, 100, 100, 0, 100, 100, 0, 0, 0, 100, 0, 0, 0, 100, 100, 100, 0, 0, 100, 0, 100, 100, 100, 0, 100, 0, 100, 100, 100, 0, 0, 0, 0, 0, 100, 100, 0, 0, 0, 100, 0, 100, 0, 0, 0, 100, 100, 100, 100, 100, 100, 100, 100, 0, 0, 0, 100, 100, 100, 0, 100, 0, 100, 100, 0, 100, 0, 0, 100, 100, 0, 0, 100, 100, 0, 100, 100, 100, 100, 100, 0, 0, 100, 100, 100, 100, 0, 100, 0, 100, 0, 0, 100, 100, 100, 100, 100, 0, 100, 100, 100, 100, 100, 100, 0, 0, 0, 100, 0, 100, 0, 100, 0, 0, 0, 100, 100, 100, 0, 0, 0, 100, 0, 100, 0, 100, 100, 0, 0, 100, 0, 100, 100, 100, 100, 100, 0, 0, 0, 0, 0, 100, 0, 100, 100, 0, 0, 0, 100, 0, 0, 100, 100, 0, 0, 0, 100, 100, 100, 0, 0, 100, 100, 0, 0, 0, 0, 100, 0, 100, 0, 0, 100, 0, 100, 100, 0, 0, 0, 100, 0, 0, 100, 100, 0, 0, 0, 100, 100, 100, 0, 100, 0, 0, 0, 0, 100, 0, 100, 0, 100, 0, 0, 0, 100, 100, 100, 0, 0, 0, 0, 100, 100, 0, 100, 0, 100, 0, 0, 0, 100, 0, 100, 0, 0, 100, 100, 100, 0, 100, 100, 100, 100, 100, 0, 100, 0, 100, 0, 0, 100, 100, 0, 100, 0, 0, 0, 100, 100, 100, 100, 0, 0, 100, 0, 100, 100, 100, 100, 0, 100, 0, 100, 0, 0, 100, 0, 100, 0, 0, 100, 100, 0, 100, 0, 100, 100, 0, 100, 100, 100, 100, 100, 100, 100, 100, 100, 100, 100, 100, 100, 0, 0, 100, 0, 100, 0, 100, 100, 100, 100, 100, 100, 100, 0, 100, 0, 0, 100, 100, 100, 100, 0, 100, 0, 100, 100, 100, 0, 100, 100, 100, 0, 0, 100, 100, 100, 100, 0, 0, 0, 0, 100, 0, 0, 100, 0, 100, 100, 100, 0, 100, 100, 0, 0, 0, 100, 0, 0, 0, 0, 0, 100, 100, 100, 100, 100, 0, 0, 100, 0, 0, 0, 100, 100, 100, 100, 100, 100, 0, 100, 0, 100, 0, 0, 100, 100, 0, 0, 0, 0, 100, 100, 100, 0, 100, 100, 100, 0, 100, 100, 0, 100, 100, 100, 0, 0, 100, 0, 0, 0, 100, 100]